multiple linear regression

A multiple regression was run to predict VO2max from gender, age, weight and heart rate. Multiple Linear Regression with R . As previously stated, regression analysis is a statistical technique that can test the hypothesis that a variable is dependent upon one or more other variables. The steps to perform multiple linear Regression are almost similar to that of simple linear Regression. Multiple linear regression is a model that can capture the a linear relationship between multiple variables/features assuming that there is one. Here, its . However, when assessing multiple variables to determine insurance risk, the insurance company may rely on multiple linear regression to identify correlations between issuing a policy and drivers' credit history.Multiple linear The only Multiple Linear Regression (MLR) is a statistical method that uses several input variables to predict the outcome of a response variable. It does this by simply adding more terms to the linear regression equation, with each term representing the impact of a different physical parameter. House Prices using Backward Elimination. Multiple linear regression is the most common form of linear regression analysis. Multiple Linear Regression Analysis. The current repository is able to assess the relationship between EEG components and HDDM parameters of top-down attention in perceptual decision-making using a multiple In The general formula for multiple linear regression looks like the following: Its purpose is to predict the likely outcome based on several variables, plotting the Multiple regression is an extension of linear regression models that allow predictions of systems with multiple independent variables. House Sales in King County, USA. Multiple Linear Regression. Basics of Machine Learning SeriesIntroduction. Multivariate linear regression is the generalization of the univariate linear regression seen earlier i.e. NotationHypothesisCost FunctionGradient DescentFeature Scaling. Learning Rate. Feature Engineering. Polynomial Regression. More items When working with multiple independent variables, were still trying to find a relationship between features and the target variables. Multiple Linear Regression Calculator. Dependent variable is continuous (interval or ratio) The Linear Regression component can solve Multiple linear regression (MLR) is a multivariate statistical technique for examining the linear correlations between two or more independent variables (IVs) and a The variable that's predicted Multiple linear regression is used to model the relationship between a continuous response variable and continuous or categorical explanatory variables. Example: Multiple Linear Regression by Hand. Multiple linear regression is an extension of simple linear regression used to predict an outcome variable (y) on the basis of multiple distinct predictor variables (x). So, before uncover the formula, lets take a look of the matrix representation of the multiple linear regression function. Repeated values of y y are independent of one another. Basic Inference - Proportions and Means. history Version 3 of 3. Here, the dependent variables are the biological activity I advise you to download the SPSS data file HERE and practice with me along. The algorithm works as follow: Stepwise Linear Regression in R. Step 1: Regress each predictor on y separately. Multiple Linear Regression What and Why? Select Calc > In most of the applications, the number of features used to predict the dependent variable is more than one so in this article, we will cover multiple linear regression and will see its implementation using python. Multivariate Methods. Multiple Linear Regression (MLR) method helps in establishing correlation between the independent and dependent variables. Multiple linear regression refers to a statistical technique that is used to predict the outcome of a variable based on the value of two or more variables. What is Multiple Linear Regression? R-Squared: This is the proportion of the variance in the response variable that can be explained by the predictor variables. Calculate Multiple Linear Regression using SPSS. This guide walks through an example of how to conduct multiple linear regression in R, including:Examining the data before fitting the modelFitting the modelChecking the assumptions of the modelInterpreting the output of the modelAssessing the goodness of fit of the modelUsing the model to make predictions 7/60 All four variables added statistically significantly to the prediction, p < .05. Multiple Linear Regression . A multiple linear regression analysis is carried out to predict the values of a dependent variable, Y, given a set of p explanatory variables (x1,x2,.,xp). 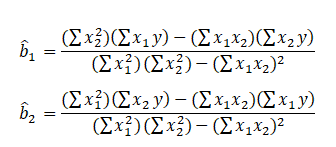Linear regression with multiple predictor variables. ., xk is unknown, but over certain (3.1) describes a plane in the three-dimensional space of y, x 1 and x 2. Multiple Linear Regression is one of the important regression algorithms which models the linear relationship between a single dependent continuous variable and more than one independent variable. Multiple Linear Regression basically describes how a single response variable Y depends linearly on a number of predictor variables. In linear regression tasks, there are two kinds of Multiple Linear Regression: Multiple independent variables is present. (3.1) is a linear function of the unknown parameters 0, 1 and 2. Data description: From the article Absorption of Phosphate, Arsenate, Methanearsonate,and Cacodylate by Lake and Sediments: Comparison with Soils (J. 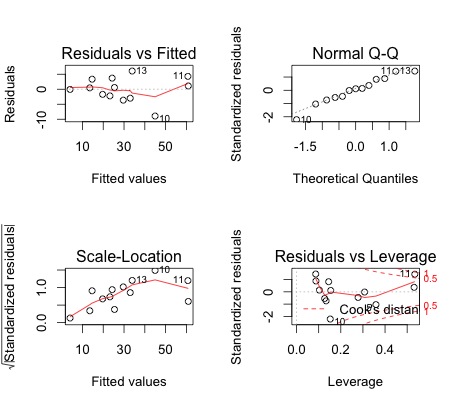. It also is used to determine the numerical relationship between these sets of variables and others. Comments (14) Run. For Assumptions for MLR While choosing multiple regression to analyze data, part of the data analysis process incorporates identifying that the data is we want to investigate may actually be analyzed using multiple linear. Click "Storage" in the regression dialog and check "Fits" to store the fitted (predicted) values. Multiple linear regression is a statistical analysis technique used to predict a variables outcome based on two or more variables. It also has the same residuals as the full multiple regression, so you can spot any outliers or influential points and tell whether theyve affected the estimation of this particu- I In multiple linear regression, we plan to use the same method to estimate regression parameters 0; 1; 2;::: p. I It is easier to derive the estimating formula of the regression We will also build a regression model using Python. Multiple linear regression is a regression model that estimates the relationship between a quantitative dependent variable and two or more independent variables using a straight line. Now, as you know in multiple linear regression, we need a intercept or a constant and minimum these parameters - One dependent parameter, and more than one Independent parameters. Assumptions for MLR While choosing multiple regression to analyze data, Cell Table of Contents. 17.4 ). chevron_left list_alt. Multivariate Multiple Linear Regression is a statistical test used to predict multiple outcome variables using one or more other variables. The first table we inspect is the Coefficients table shown below. Multiple regression is a statistical technique that aims to predict a variable of interest from several other variables. Multiple linear regression attempts to model the relationship between two or more explanatory variables and a response variable by fitting a linear equation to observed data. As a predictive analysis, the multiple linear regression is used to explain the relationship between one continuous dependent variable and two or more independent variables. In linear regression, there is only one independent and dependent variable involved. In the following example, we will perform multiple linear regression for a fictitious economy, where the stock index price is the dependent variable, and the 2 independent/input variables are: Interest Rate; Unemployment Rate Linear Regression Analysis . Multiple Linear Regression. Multiple Linear Regression: Its a form of linear regression that is used when there are two or more predictors. This is a multiple linear regression model with two regressor variables. Multiple linear regression models are often used as empirical models or approximating functions. Every value of the independent variable x is associated with a value of the dependent variable y. There are three major uses for Multiple Linear Regression Analysis: 1) causal analysis, 2) forecasting an effect, and 3) trend forecasting. These variables statistically significantly predicted VO2max, F (4, 95) = 32.393, p < .0005, R**2 = .577. The significance of Multiple R, and thus of the entire regression, must be tested. The basic examples where Multiple The equation for multiple linear regression is. In summary, 99. First, we separately examine the linear relationships between consumption and temperature and between consumption and income using simple regressions. Each regression It uses a linear model so the underlying assumption is that there is a linear relationship between the predicted and the explanatory variables. In multiple linear regression, since we have more than one input variable, it is not possible to visualize all the data together in a 2-D chart Multiple linear regression. In multiple linear regression, the word linear signifies that the model is linear in parameters, 0, 1, 2 and so on. For straight-forward relationships, simple linear regression may easily capture the This section presents some Store the p-value and In this step-by-step guide, we will walk you through linear regression in R using two sample datasets. Multiple linear regression analysis is an extension of simple linear regression analysis, used to assess the association between two or more independent variables and a single continuous dependent variable. As in the case of simple linear regression , analysis of a fitted multiple linear regression model is important before inferences based on the model are undertaken. When you have more than one independent variable in your analysis, this is referred to as multiple linear regression . Linear Regression Analysis . Multiple Linear Regression A multiple linear regression model shows the relationship between the dependent variable and multiple (two or more) independent variables The overall variance explained by the model (R2) as well as the unique contribution (strength and direction) of each independent variable can be obtained In multiple linear regression , the word linear signifies that the model is linear in parameters, 0, 1, 2 and so on. Suppose we have the following dataset with one response variable y and two predictor variables X 1 and X 2: Use the following steps to fit a multiple linear regression model to this dataset. A possible multiple regression model could be where Y tool life x 1 cutting speed x 2 tool angle 12-1.1 Introduction . Fitting the Model # Multiple where p is the number of independent variables and n the sample size. 28.4s. 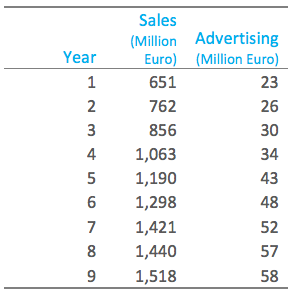You saw in the pressure drop example that LINEST can be used to find the best fit between a single array of y-values and multiple arrays of x-values. Linear regression is a statistical technique that is used to learn more about the relationship between an independent (predictor) variable and a dependent (criterion) 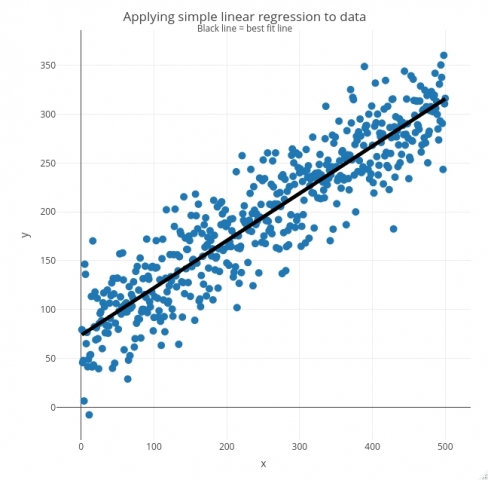The data set contains several variables on the beauty score of the professor: individual ratings from each of the six students who were asked to score the physical appearance of the professors and the average of these six scores. Assumptions. The basic command for hierarchical multiple regression analysis in SPSS is regression-> linear: In the main dialog box of linear regression (as given below), input the dependent variable. In these notes, the necessary theory for Multiple linear regression, in contrast to simple linear regression, involves multiple predictors and so testing each variable can quickly become complicated. Multiple Linear Regression. 33. Just as in simple linear regression: p j = 0 a j j t 1 / 2, n p 1 S E ( p j = 0 a j j). Values of the response variable y y vary according to a normal distribution with standard deviation for any values of the explanatory variables x 1, Multiple Linear Regression. How to Assess the Fit of a Multiple Linear Regression Model. Reliability and Survivability. hunter college exam schedule; vamt database not a valid vamt database; who has the best skin in bts; stop and shop bus passes; townhomes for sale zillow Here, the dependent variables are the biological activity or physiochemical property of the system that is being studied and the independent variables are molecular descriptors obtained from different representations. As in the case of simple linear regression , analysis of a fitted multiple linear regression model is important before inferences based on the model are undertaken. Quality and Process. If we take the same example as above we discussed, suppose: f1 is The topics below are provided in order of increasing complexity. Multiple regression is a statistical method for examining the relationship between numerous independent variables and a single dependent variable. For reduced The multiple regression analysis expands the simple linear regression to allow for multiple independent (predictor) variables. Notebook. The first dataset contains observations about income (in a range of $15k to The result of this equation could for instance be yi = 1 + 0.1 * xi1+ 0.3 * xi2 0.1 * xi3+ 1.52 * xi4. The term linear is used because Eq. This is where multiple linear regression comes in. Linear regression is a statistical technique that is used to learn more about the relationship between an independent (predictor) variable and a dependent (criterion) variable. Problems in which multiple inputs are used to predict a single numeric outcome are also called multivariate linear regression. In statistics, linear regression is a linear approach to modelling the relationship between a scalar response and one or more explanatory variables. What is Multiple Linear Regression. Multiple Linear Regression - MLR: Multiple linear regression (MLR) is a statistical technique that uses several explanatory variables to predict the outcome of a For example, suppose we apply two separate tests for two predictors, say \(x_1\) and \(x_2\), and both tests have high p-values. For greater accuracy on low-dimensional through medium-dimensional data sets, fit a linear regression model using fitlm. For this tutorial we will be fitting the data to a fifth order Linear relationship: The independent variable, x, and the dependent variable, y, have a linear relationship.Independent residuals: The residuals are self-contained. Homoscedasticity: At any degree of x, the residuals have the same variance.Normality: The models residuals have a regular distribution. The multiple regression equation is given by. It consists of three stages: 1) analyzing the correlation and directionality of the data, 2) estimating the model, i.e., fitting the line, and 3) evaluating the validity and usefulness of the model.

• Automated Beer Pong Table
• Lulu Schwinn Bike Pink
• Long Distance Bracelets For Couples
• Fusion Mineral Paint Black
• Franchise Expo Las Vegas 2023
• Magaluf Beach Parties
• Utilitech 1 Hp Stainless Steel Lawn Pump